this moving-around-of-letters
activity of the past couple of
rambles is, or could and (i hope
someday to convince *some*body)
should be, as foundational
in the study of mathematics as
elementary arithmetic (+, -, *, 1/n) or
compass-and-straightedge constructions.
“trust the code” shall be
the whole of the law whenever
*i* set up as math dictator.
this means symbol-by-symbol
every-keystroke-perfect *code*
is, first of all our *subject matter*
when we’re studying algebra
every bit as much as it is for its
johnny-come-lately derivative
“computer programming” (whatever
the proper euphemism is these days).
enforcing this level of attention to
detail *without* a computer turns out
to be quite difficult. one of the great
frustrations of my life is that *with*
a computer you can pretty much get
*any*body to perform rituals of
*arbitrary* complexity as long
as no actual *reasoning* is involved
just by convincing them that there’s
a paying job in it for them somewhere
if only way down the line behind all
those other poor desparate bastards
that already graduated and have nothing
better to do now but spy on *them*.
but computers are are hard.
to pay for. to understand.
and altogether *impossible*
to maintain for long.
whereas the game
is “simple things first”.
(another fine game is
“don’t let machines
tell you how to live”.
this one’s *much* harder.)
*you can do this*.
what’s more, having done it…
and had the right *conversations*…
you’ll be darn *sure* you can.
and when anybody else…
human or robot overlord
or one of the many blends
emerging all around us daily…
has it *wrong*, you’ll *know*.
here is power.
*that*’s what the simplicity is for.
let me go ahead here and admit that
there’s plenty of good math you can do
*without* this almost-machine-code
letter-by-letter detail-oriented
okay-i-admit-even-somewhat-obsessive
*algebra* stuff.
i was an algebra *major*. so i’m biased.
anyway, logicians are worse. but no. really.
this is the stuff that’ll make you *good*.
story-of-the-blog-so-far stuff.
last winter when i was blogging
about my math148 precalculus class
(as i think of it; three classes really),
i devoted quite a bit of attention to
finding and implementing the “right”
notation for, what was one of
the big themes of the course,
transformations of the xy-plane.
here as maybe nowhere else
one has an opportunity to *use*
the “points as ordered pairs”
point-of-view so sloppily
developed throughout math101.
because the centerpiece
in everybody *else’s* imagination
seems to be the xy-plane
itself… the admittedly epoch-making
observation that by laying down
co-ordinates over a euclidean plane
you get a cartesian plane and all
of a sudden equations have *pictures*.
ooo. aaah.
and these pictures are all well and good
and the basis for the scientific revolution
whether *i* like it or not and all that.
but.
the kids don’t get it. and won’t
until they believe they can. and
as to “functions as sets of ordered pairs”,
the examples given typically…
graphs of polynomials and whatnot…
have manymany scary confusing aspects
already known by the audience to be
well beyond their comprehension.
so it’s… well… just *logic*
(not *rocket science*[!]): simple
things first. confused about why
some “transformation” (that doesn’t
even have a proper name, let
alone appropriate symbol)
causes “it” (the graph of…
something… but “it” isn’t usually
any one thing in these discussions)
to *change* in some particular way?
well, how about a bunch of highfalutin
*technical terms* that you know very
well *you* don’t know (and have no
very good reason to be sure about
the teacher)? that’ll sure be useful.
(depending on your goals.)
confused about A, B, and C?
*where*, precisely?
how did *yours* look?
in the *spirit* of “keep it simple”
i now propose to ramble some more
about the “simplest interesting case”
of permuting the elements of a set:
the case of *three* elements.
ABC ACB BAC BCA CAB CBA
XYZ XZY YXZ YZX ZXY ZYX
here are two isomorphic “strings”.
“isomorphic” means “having the same form”.
that the strings… lists of symbols…
*do* have the same form
in some sense is probably obvious to
any reader. heck, six groups of three.
but more than this.
the set isomorphism



“induces” (what i’m here calling)
an isomorphism of lists:
replacing each left-hand object
wherever it appears in
our first string with the
corresponding right-hand object
produces the second string.
note that “isomorphism of sets”
is (and deserves to be) standard language
for the kind of one-to-one (and “onto”)
function we’ve displayed here.
two (finite) sets “are isomorphic”
as soon as they have the same number
of elements.
but there will be many different
isomorphisms between any
pair of isomorphic sets.
indeed… theorem 1!… there’ll
be n! (en-factorial) of ’em
between any pair of n-element
sets. (you see this, right?…
remember that factorials count
permutations…)




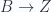
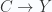




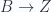



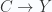



.
now. in the spirit of the introductory
ramble from a couple weeks back.
two exercises are isomorphic
when one can be worked out from the
solution of the other simply by
replacing “letters”.
consider the six isomorphisms
from {A, B, C} to {X, Y, Z}
(as shown above).
for a low pass, write out all six
isomorphisms from {a, b, c} to {x, y, z}.
for a passing grade, write out all
six isomorphisms from {P,D,Q} to {E,I,O}.
let (the particular isomorphism)

be denoted by “elbowgrease”.
write out the result of applying
elbowgrease to the string PDPDQ.
for a high pass write out the
iso’s from {1,2,3,4} to itself.
what happens if you “apply”
an isomorphism to the result
of the application-of-an-iso’ism?
for a pass with distinction learn
“cycle” notation and how to calculate
with isomorphisms-of-sets considered
as members of the so-called
symmetric group on three elements.
essay question for advanced credit.
we’ve “gone meta” twice in “lifting”
correspondences of sets first
to what we called isomorphisms
of strings, and then to
isomporphisms of exercises.
one could continue to “lift” the
concept to even “higher-level”
groups of data… perhaps introducing
some metaphor along the way to
replace strict symbol-for-symbol
sustitution.
find a pair of textbooks covering
transformations of the plane.
display an “isomorphism” between
the bone-headed wrong ways the
relevant sections of your chosen
texts leave out crucial concepts and
fudge important details.
develop a theory of how this state
of affairs came about. for the
love of god and the gratitude
of generations still to come
do something to change it.